Accelerated Algebra/Geometry Trig Ratios Practice: Essential Guide for Success sets the stage for this enthralling narrative, offering readers a glimpse into a story that is rich in detail and brimming with originality from the outset. The significance of practicing accelerated algebra/geometry trig ratios cannot be overstated, as it provides a solid foundation for understanding complex mathematical concepts and their applications in real-world scenarios.
This comprehensive guide delves into the fundamental concepts of trigonometric ratios, providing clear definitions and real-world examples to illustrate their significance. It also Artikels a comprehensive practice plan, including effective methods for practicing trig ratios through drills, exercises, and problem-solving.
Accelerated Algebra/Geometry Trig Ratios Practice: Overview
Accelerated algebra/geometry trig ratios practice is essential for students seeking to enhance their understanding of trigonometric concepts and develop problem-solving skills. It provides a solid foundation for advanced mathematical studies and practical applications in various fields.
By engaging in accelerated practice, students can improve their:
- Understanding of the fundamental concepts of trigonometry
- Ability to apply trig ratios to real-world scenarios
- Problem-solving skills and critical thinking abilities
- Preparation for standardized tests and higher-level mathematics courses
Key Concepts in Trig Ratios
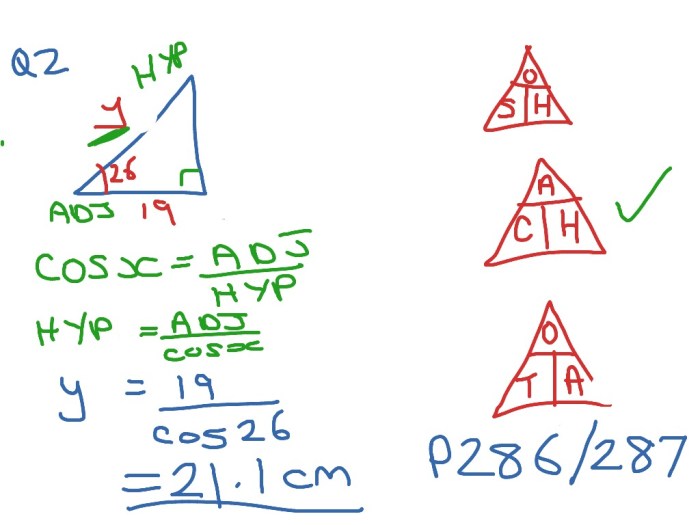
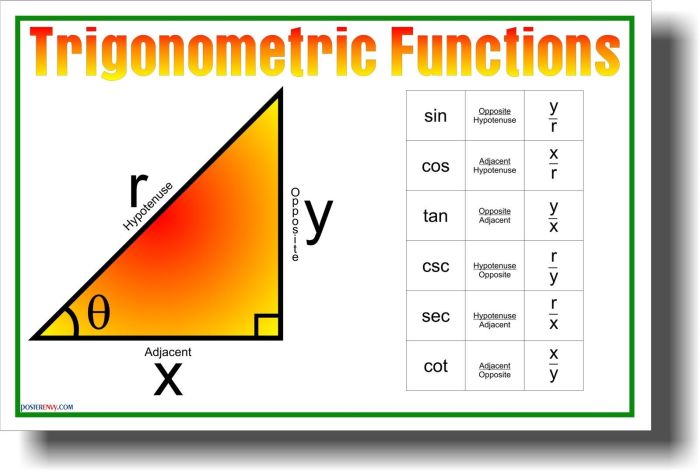
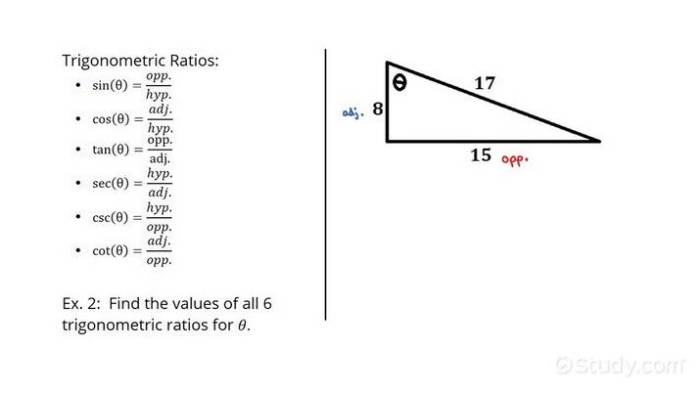
Trigonometric ratios (sin, cos, tan, etc.) are mathematical functions that relate the angles of a right triangle to the lengths of its sides. These ratios are:
- Sine (sin):Opposite side / Hypotenuse
- Cosine (cos):Adjacent side / Hypotenuse
- Tangent (tan):Opposite side / Adjacent side
Trig ratios are used to solve problems involving:
- Angle measurement
- Side lengths of triangles
- Heights and distances
Practice Methods for Trig Ratios
Effective trig ratio practice involves:
- Regular drills:Practice problems daily to improve fluency and recall.
- Exercises:Solve more complex problems to apply concepts and develop problem-solving skills.
- Problem-solving:Engage in real-world scenarios that require the application of trig ratios.
- Technology:Utilize online resources and apps for interactive practice and feedback.
Applications of Trig Ratios
Trig ratios have numerous applications in:
- Architecture:Calculating heights and angles of buildings
- Engineering:Designing bridges, calculating forces, and analyzing structures
- Navigation:Determining distances, angles, and positions on maps and in the sky
- Astronomy:Measuring distances to stars and planets
- Music:Calculating frequencies and intervals
Tips for Effective Practice, Accelerated algebra/geometry trig ratios practice
- Set realistic goals:Start with small practice sessions and gradually increase difficulty.
- Seek feedback:Ask teachers or tutors for guidance and review.
- Stay motivated:Find ways to make practice engaging, such as using games or real-world examples.
- Review regularly:Revisit concepts and practice problems to reinforce learning.
- Use technology:Explore online resources and apps to enhance practice and provide instant feedback.
FAQ Summary: Accelerated Algebra/geometry Trig Ratios Practice
What are the benefits of practicing accelerated algebra/geometry trig ratios?
Practicing accelerated algebra/geometry trig ratios enhances problem-solving skills, improves spatial reasoning, and strengthens the foundation for advanced mathematical concepts.
How can I effectively practice trig ratios?
Engage in regular drills, solve practice problems, and utilize online resources to reinforce your understanding.
Where are trig ratios applied in real-world scenarios?
Trig ratios find applications in architecture, engineering, navigation, and many other fields.